
The Monster of The Coin
A brief investigation into the nature of the random (and the extent of human gullibility)
By Sergio Navega snavega@attglobal.net
http://www.intelliwise.com/snavega
July 2000
This is a Preliminary Draft, Under Construction, comments welcome
It is surprising how often we find interesting patterns when we look at natural scenes. We frequently find shapes of faces drawn by clouds, branches of trees moving like a threatening monster or funny figures sculpted in rocks and mountains. However surprising these suggestive figures might be, there's something that would be even more surprising: if we didn't find them at all. The nature of random processes is such that it is very likely that we find these figures now and then, and it is very unlikely that we find patterns which can't be interpreted in one way or another.
The role of the interpreter in this scheme of things is one of the points of this article. Patterns don't exist outside the mind of a sentient organism. If one person sees a cloud with a shape resembling a face, another person may not see it immediately. We can say that the former has the necessary perceptual preconditions to construct that image, while the latter don't. But once the latter is guided to specific parts of the image (the tip of the nose, the hollowness of the mouth, etc), then suddenly all comes into place and the whole figure is perceived. This gestaltic effect of sudden perception of the whole has been studied for decades and has recently been explained as a synchronous activity of groups of neurons, where each group is specialized into the recognition of a specific feature (Singer 1999, Varela et al. 1999).
Brains are not only pattern seekers, but also pattern fillers. One of the fundamental activities of perceptual systems is to be efficient in recognizing regular structures. But this is not its only ability: perceptual systems also excel on the completion of partial patterns. Typical examples like the Kanizsa triangle (below) show that there are some important reasons for our compulsion to fill patterns (Pessoa 1998).

This phenomenon has been shown to happen also within the auditory domain, where filtering of sounds may not only alter our ability to locate its real position, but also to create illusions of sources that don't exist (Xu et al. 1999).
The Problematic Claim
Pseudo-science is fertile with examples of patterns found in the middle of noise. I will direct our attention to the "instrumental transcomunication" researchers, who frequently find faces of people, monsters and all sort of figures in recordings of video cameras. These cameras feed back their signal to the television they're pointing at. The huge number of patterns produced by this method (because of the non-linear nature of this feedback loop) reveal quite lot of material for our minds to delve into. They claim that some of these patterns are not (or could not) be artifacts of randomness, but are real communications of the spirits of dead people. There are some ideas that could be put forth in order to contest these claims, but let's focus here on the question of probability: how likely is it to obtain face-like figures from pure random data?
An Experiment With Randomness
I devised a simple experiment to try to find patterns in random sequences. Instead of using a sophisticated recording equipment, I just flipped a coin 110 times, annotating the result (table below).
H T T H T H T H H H T T T H T H H H T HNext, I divided this sequence into 11 groups of 10 each, composing a matrix like this:
HTTHTHTHHHFor each "Head", I drew a small white square, for each "Tail", I drew a black square. This transformed our matrix into the following image:

This image, as we have seen, is the result of a random process of tossing coins. Now comes another detail of the story. Most processes in nature are composed of probabilistic distributions around one central average. One of the distributions frequently found in natural processes is that of a normal or gaussian curve. If we take this image and pass it through a gaussian filter, we get this image:

The image is nothing more than a mere filtering over randomly obtained data. Nevertheless, it is possible to obtain meaningful sub-images, by focusing our attention to specific parts. Add a bit of noise and we obtain what I'm calling (for lack of a better name) "the monsters of the coin":

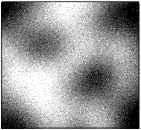
So how unlikely is it for us to obtain face-like figures from a sequence of random events? It is very likely indeed! It would be odd if it were otherwise. It all comes as the result of our tendency to find familiar structures in unfamiliar data. Take this tendency in conjunction with our illusions of assessment of probability and we have an improper way to justify even the improbable. For instance, one would think that this pattern:
HTTTTTTTTTTTTTTTTTTTTTTTTTTTH
would be much less likely to obtain than this one:
HTHTHTHTHTHTHTHTHTHTHTHTHTHTH
which will be less likely than this one:
HTTTHTHHTTHTHTTHTTHTHHTTHHTTT
However, the probability of obtaining any of (exactly) these patterns by tossing a fair coin is exactly the same. In fact, one notion frequently seen as surprising about random distributions is that the probability of obtaining any finite pattern (no matter the size or the sequence of heads and tails, as long as it is finite) in an infinite sequence of coin tosses is exactly 1.00 (see, for instance, Stewart 1998).
In summary, patterns are a dime a dozen, and this is a concept that we should carry with us. When analyzing data that appears to mean something, it pays to use the scientific method, where we look not only for patterns, but also causal models and predictive power. This is the best way we have so far to advance one's knowledge without being misled by our strong tendency of finding meaning in patterns.
References
Pessoa, Luiz; Neumann, Heiko (1998) Why does the brain fill in?. Trends in Cognitive Science, Vol 2, No. 11, Nov 1998.
Stewart, Ian (1998) Repealing the Law of Averages. Scientific American, April 1998.
Singer, Wolf (1999) Striving for coherence. Nature 397, 391 - 393 (04 Feb 1999).
Varela, Francisco J. (et al.) (1999) Perception's shadow: long-distance synchronization of human brain activity. Nature 397, 430 - 433 (1999)
Xu, Li; Furukawa, Shigeto; Middlebrooks, John C. (1999) Auditory cortical responses in the cat to sounds that produce spatial illusions. Nature Vol 399, 17 Jun 1999.